Angular Displacement Formulas and Solved Exercises
den vinkelforskydning det genereres, når et objekt bevæger sig efter en sti eller sti, der har form af en cirkel. Det er forskelligt fra forskydningen; mens vinkelforskydningen måler vinklen, måler forskydningen afstanden.
For at beregne vinkelforskydningen af et objekt, som bevæger sig langs en omkreds, kan to måder anvendes: hvis den indledende og endelige vinkel er kendt, vil vinkelforskydningen være subtraktionen mellem den endelige vinkel og den indledende vinkel.
Hvis længden af forskydningen (længden af den periferiske bue rejst) og radiusen af omkredsen er kendt, er vinkelforskydningen givet med θ = l / r.
indeks
- 1 formler
- 2 øvelser
- 2.1 Første øvelse
- 2.2 Anden øvelse
- 2.3 Tredje øvelse
- 3 referencer
formler
For at opnå de ovenfor beskrevne formler kan du se følgende billeder:
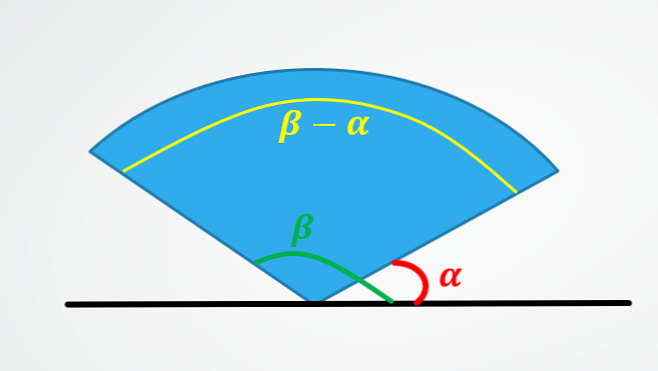
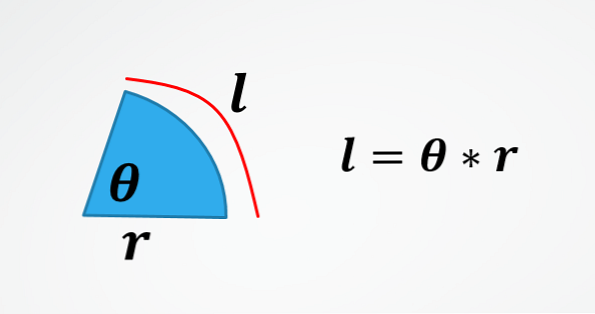
Den første viser hvorfor vinkelforskydningen er lig med subtraktionen af den endelige vinkel minus den indledende vinkel.
I det andet billede er formlen for længden af en cirkelbue. Derfor ved at rydde θ får du den beskrevne formel i begyndelsen.
uddannelse
Nedenfor er nogle øvelser, hvor definitionen af vinkelforskydning skal anvendes, og hvor de ovenfor beskrevne formler anvendes.
Første øvelse
Juan har kørt en afstand på 35 meter på et cirkulært løbespor, hvis radius er lig med 7 meter. Beregn den vinkelforskydning, som Juan har lavet.
opløsning
Da afstanden af buen rejste og omkredsens radius er kendt, kan den anden formel anvendes til at kende vinkelforskydningen lavet af Juan. Ved at bruge formlen beskrevet ovenfor har du det θ = 35/7 = 5 radianer.
Anden øvelse
Hvis du har, at Mario har rejst i hans køretøj halvdelen af et cirkulært løb, hvad er den vinkelforskydning, Mario har gjort??
opløsning
I denne øvelse anvendes den første formel. Da det er kendt, at Mario har rejst halvdelen af banen, kan det antages, at han startede løbet i 0 ° vinklen, og da han nåede midt i cirklen, har han rejst 180 °. Svaret er derfor 180 ° -0 ° = 180 ° = π radianer.
Tredje øvelse
María har en cirkulær pool. Din hund løber rundt om poolen, der dækker en afstand på 18 meter. Hvis poolens radius er 3 meter, hvad er vinkelforskydningen foretaget af Marias maskot??
opløsning
Da poolen er cirkulær og du kender radius af det, kan du fortsætte med at bruge den anden formel.
Det er kendt, at radiusen er lig med 3 meter, og den afstand, der tilbagelægges af kæledyret, er lig med 18 meter. Derfor udføres den vinkelforskydning, der er θ = 18/3 = 6 radianer.
referencer
- Basto, J.R. (2014). Matematik 3: Grundlæggende analytisk geometri. Patria Editorial Group.
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematik: en problemløsende tilgang til grundlærere. López Mateos Editores.
- Bult, B., & Hobbs, D. (2001). Math leksikon (illustreret udgave). (F. P. Cadena, Trad.) Udgave AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometri. Reform af den øvre cyklus af E.G.B. Undervisningsministeriet.
- Schneider, W., & Sappert, D. (1990). Praktisk teknisk tegning manual: Introduktion til det grundlæggende i industriel teknisk tegning. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Beregning: flere variabler. Pearson Education.


