Archimedes Biografi, Bidrag og Opfindelser
Archimedes of Syracuse (287 a.c. - 212 a.C.) var en matematiker, fysiker, opfinder, ingeniør og græsk astronom fra den gamle by Syracuse på øen Sicilien. Hans mest fremragende bidrag er princippet om Archimedes, udviklingen af exhaution-metoden, den mekaniske metode eller oprettelsen af det første planetarium.
I øjeblikket betragtes det som et af de tre vigtige figurer i antikkens matematik ved siden af Euclides og Apolonio, da dets bidrag betydede vigtige videnskabelige fremskridt for tiden inden for beregning, fysik, geometri og astronomi. Til gengæld gør dette ham til en af de mest fremragende forskere i menneskehedens historie.

Selvom nogle detaljer i hans personlige liv og de kendte er tvivlsomme pålidelighed kendte, er deres bidrag kendte takket være en række skriftlige breve om deres arbejde og resultater, der er blevet bevaret indtil i dag, tilhører til korrespondancen, som han holdt i årevis sammen med venner og andre matematikere af tiden.
Archimedes var berømt i sin tid takket være hans opfindelser, som tiltrak hans samtidige opmærksomhed, dels fordi de blev brugt som krigsindretninger for heldigvis at undgå mange romerske invasioner..
Det siges imidlertid, at han hævdede, at den eneste rigtig vigtige ting var matematik, og at hans opfindelser kun var et produkt af tidsfordrivet af anvendt geometri. I eftertiden har hans værker i ren matematik været meget mere værdsat end hans opfindelser.
indeks
- 1 Biografi
- 1.1 Uddannelse
- 1.2 Videnskabeligt arbejde
- 1.3 Konflikt i Syracuse
- 1.4 Dødsfald
- 2 Arkimedes videnskabelige bidrag
- 2.1 Archimedes princip
- 2.2 Mekanisk metode
- 2.3 Forklaring af armens lov
- 2.4 Udvikling af udtømnings- eller udtømningsmetoden til den videnskabelige demonstration
- 2.5 Målingen af cirklen
- 2.6 Geometrien af kugler og cylindre
- 3 opfindelser
- 3.1 Kilometertælleren
- 3.2 Det første planetarium
- 3.3 Archimedes skruen
- 3.4 Archimedes klo
- 4 referencer
biografi
Archimedes of Syracuse blev født cirka i år 287 f.Kr. Ikke meget information er kendt om hans tidlige år, selv om det kan siges at han blev født i Syracuse, en by betragtes som den største havn på øen Sicilien, i dag i Italien..
På den tid var Syracuse en af de byer, der bestod af den såkaldte Magna Grecia, som var rummet beboet af bosættere af græsk oprindelse til det sydlige område af halvøen i Italien og på Sicilien.
Der er ingen kendte fakta om Archimedes mor. I forhold til faderen er det kendt, at dette blev kaldt Phidias, og at han var dedikeret til astronomi. Denne information fra sin far er kendt takket være et fragment af bogen Sandtælleren, skrevet af Archimedes, hvor han nævner sin fars navn.
Heraklides, som var en græsk filosof og astronom, var meget glad for Archimedes og selv skrev en biografi om ham. Dette dokument er imidlertid ikke bevaret, så al informationen deri er ukendt.
Desuden historikeren, filosof og biografi Plutarch erklærede i sin bog Parallel Lives at Archimedes blev fortalt af blod til Hiero II, en tyran som befalet i Syracuse siden 265 f.Kr..
uddannelse
Som et resultat af den lille information, vi har om Archimedes, ved vi ikke sikkert hvor han fik sin første træning.
Imidlertid har forskellige historiografer fastslået, at Archimedes har en stor mulighed for at studere i Alexandria, som var det vigtigste græske kultur- og undervisningscenter i regionen..
Denne antagelse støttes af de oplysninger, som den græske historiker Diodoro Sículo tilbød, der angav, at Archimedes sandsynligvis studerede i Alexandria.
Desuden nævner Archimedes selv i mange af hans værker andre videnskabsmænd af den tid, hvis arbejde var koncentreret i Alexandria, så det kan antages, at han faktisk udviklede sig i den by.
Nogle af de personligheder, som Archimedes menes at have interageret med i Alexandria, er geometrien, matematikeren og astronomen Eratosthenes fra Cyrene, og matematikeren og astronomen Conon de Sanos.
Familie motivation
På den anden side, det faktum, at Archimedes' far var en astronom kan have påvirket betydeligt i de tilbøjeligheder senere demostróe fordi senere og fra en ung alder, var tydelig i ham en særlig attraktion til området for videnskab.
Efter sin tid i Alexandria anslås det, at Archimedes vendte tilbage til Syracuse.
Videnskabeligt arbejde
Efter at have vendt tilbage til Syracuse begyndte Archimedes at udtænke forskellige artefakter, der snart vandt ham en vis popularitet blandt indbyggerne i denne by. I denne periode gav han sig helt til videnskabeligt arbejde, producerede forskellige opfindelser og udledte flere matematiske forestillinger meget avancerede til sin tid.
For eksempel, da han dedikerede sig til undersøgelsen af egenskaberne ved solide buede og flade figurer, kom han op på begreber relateret til integral- og differentialkalkulator, som blev udviklet senere.
Archimedes var også den, der definerede, at volumenet forbundet med en kugle svarer til dobbelt så stor som den cylinder, der indeholder den, og var den, der opfandt den kompositskive, baseret på hans opdagelser om loven af armen.
Konflikt i Syracuse
I løbet af året 213 f.Kr. trådte romerske soldater ind i byen Syracuse og omringede sine bosættere for at få dem til at overgive sig.
Denne handling blev ledet af militæret og den græske politiker Marco Claudio Marcelo inden for rammerne af anden punkekrig. Senere var det kendt som Romens Sværd, da det endte med at erobre Syracuse.
Midt i konflikten, der varede to år, bosiddende i Syracuse mod romerne kæmpede med mod og vildskab, og Arkimedes spillet en meget vigtig rolle, da det blev dedikeret til at skabe værktøjer og instrumenter, der hjælper med at besejre romerne.
Endelig tog Marco Claudio Marcelo byen Syracuse. Før Archimedes store intellektualitet bestilte Marcelo, at de ikke blev såret eller dræbt. Imidlertid blev Archimedes dræbt i hænderne på en romersk soldat.
død
Archimedes døde i år 212 f.Kr. Mere end 130 år efter sin død, i år 137 f.Kr., optog forfatteren, politikeren og filosofen Marco Tulio Cicero en stilling i forvaltningen af Rom og ønskede at finde Archimedes grav.
Denne opgave var ikke let, da Cicero ikke kunne finde nogen til at angive det præcise sted. Men han fik det til sidst, meget tæt på Agrigento dør og i beklagelige forhold.
Cicero rensede graven og opdagede, at den var indskrevet med en kugle inde i en cylinder, som en henvisning til opdagelsen om det omfang, Archimedes lavede for nogen tid siden..
Versioner om hans død
Første version
En af versionerne siger, at Archimedes var midt i at løse et matematisk problem, da han blev kontaktet af en romersk soldat. Det siges, at Archimedes kunne have bedt ham lidt om at løse problemet, så soldaten ville have slået ham ihjel.
Anden version
Den anden version ligner den første. Vær opmærksom på, at Archimedes løste et problem med matematik, da byen tog sted.
En romersk soldat kom ind i hans sammensætning og beordrede ham til at møde Marcelo, og Archimedes svarede, at han måtte løse det problem, han arbejdede på først. Soldaten blev forstyrret som følge af dette svar og dræbte ham.
Tredje version
Denne hypotese indikerer, at Archimedes havde i sine hænder en stor mangfoldighed af instrumenter, der er typiske for matematik. Så så en soldat ham, og han troede, at han kunne bære værdifulde ting, så han dræbte ham.
Fjerde version
Denne version illustrerer, at Archimedes blev buet tæt på jorden og overvejede planer, han studerede. Tilsyneladende kom en romersk soldat bagfra og var uvidende om, at det var Archimedes, skudt ham.
Arkimedes videnskabelige bidrag
Principen om Archimedes
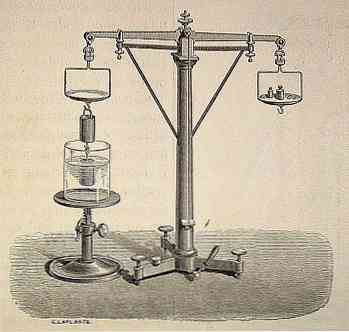
Archimedes princip betragtes af moderne videnskab som en af de ældgamle æraers vigtigste legacyer.
Gennem historien og mundtlige maneral er det blevet afleveret Arkimedes kom til hans opdagelse uheld takket være kong Hiero vil overlade kontrollere, om en guldkrone bestilt til at gøre for ham blev gjort kun guld ren og indeholdt ikke noget andet metal. Jeg måtte udføre dette uden at ødelægge kronen.
Det siges, at mens Archimedes mediterede, hvordan han skulle løse dette problem, besluttede han at tage et bad, og da han trådte ind i badekaret, indså han, at vandet steg på niveau, da han nedsænkede sig i det..
På den måde vil han opdage det videnskabelige princip om, at "hver krop nedsænket helt eller delvist i en væske (væske eller gas) modtager et opadgående tryk, svarende til vægten af væsken, der løsnes af objektet".
Dette princip betyder, at fluiderne udøver en opadgående kraft, som skubber opad-ethvert objekt nedsænket i dem, og at mængden af denne opdrift er lig med vægten af væske fortrænges af det neddykkede legeme, uanset vægt.
Forklaringen af dette princip beskriver fænomenet flotation og findes i dets Traktat om flydende organer.
Principen om Archimedes er blevet anvendt kraftigt i eftertiden for flydende genstande med massiv brug som ubåde, skibe, livreddere og balloner.
Mekanisk metode
En anden af Archimedes vigtigste bidrag til videnskaben var inddragelsen af en rent mekanisk-det er teknisk metode i argumentationen og argumentationen af geometriske problemer, hvilket betød en hidtil uset måde at løse denne type problemer for tiden.
I forbindelse med Archimedes blev geometrien betragtet som en udelukkende teoretisk videnskab, og den fælles ting var, at ren matematik stammer fra andre praktiske videnskaber, hvor dens principper kunne anvendes..
Af denne grund anses det i dag som forløber for mekanik som en videnskabelig disciplin.
I det skrift, hvori matematikeren udsætter den nye metode til sin ven Eratosthenes, indikerer det, at dette giver mulighed for at løse problemer i matematik gennem mekanik, og at det er noget lettere at bygge demonstrationen af en geometrisk sætning, hvis det allerede er Har nogle tidligere praktisk viden, at hvis du ikke har nogen ide om det.
Denne nye undersøgelsesmetode udført af Archimedes ville blive forløber for den uformelle fase af opdagelse og hypotesebeskrivelse af den moderne videnskabelige metode.
Forklaring af armens lov
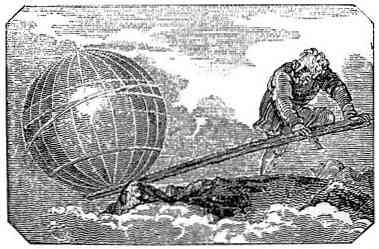
Mens armen er en simpel maskine, der blev brugt siden meget tidligere end Archimedes, var det han, der formulerede det princip, der forklarer dets funktion i sin afhandling På balancen af flyene.
I formuleringen af denne lov fastlægger Archimedes principper, der beskriver en håndtags forskellige opførsel, når de placerer to kroppe på den, afhængigt af dens vægt og afstanden fra støttepunktet.
På den måde påpeger han, at to organer, der kan måles (passende), er placeret på en håndtag, er afbalanceret, når de er i afstande, der er omvendt proportional med deres vægt.
På samme måde gør det umenneskelige organer (som ikke kan måles), men denne lov blev påviselig af Archimedes kun med organer af den første type.
Dens formulering af leveprincippet er et godt eksempel på anvendelsen af den mekaniske metode, da den ifølge en redegørelse i et brev rettet mod Dositeo blev opdaget i et første øjeblik gennem metoder af mekanikerne, der satte i praksis.
Senere formulerede han dem ved hjælp af geometriske metoder (teoretisk). Fra dette eksperiment på legemet blev også begrebet tyngdepunkt løsnet.
Udvikling af udmattelses- eller udmattelsesmetode til den videnskabelige demonstration
Udmattelse er en metode, der anvendes i geometri, der består af tilnærmelse af geometriske figurer, hvis område er kendt ved hjælp af indskriften og omskriften på en anden, hvis område er beregnet til at være kendt..
Selv om Archimedes ikke var skaberen af denne metode, udviklede han det mesterligt og formåede at beregne ved hjælp af det en præcis værdi af Pi.
Archimedes, ved hjælp af udmålingens metode, indskrev og omskriver sekskanter til en omkreds med diameter 1, hvilket reducerer til absurd forskellen mellem området af sekskanterne og omkredsområdet.
For at gøre dette, halverede han sekskanterne, der skabte polygoner på op til 16 sider, som vist i den foregående figur.
På denne måde kom han til at angive, at værdien af pi (af forholdet mellem længden af en cirkel og dens diameter) ligger mellem værdierne 3.14084507 ... og 3.14285714 ... .
Archimedes anvendte mesterligt metoden for exhaución, fordi det ikke kun lykkedes at tilnærme beregningen af værdien af Pi med en fejlmargin, der var ret lav og derfor ønsket, men også fordi Pi er et irrationelt tal gennem denne metode og de opnåede resultater lagde grundlaget, der ville spire i det uendelige kalibreringssystem og senere i den moderne integrale beregning.
Foranstaltningen på cirklen
For at bestemme en cirkels areal anvendte Archimedes en metode, der bestod i at tegne en firkant, der passer præcis inde i en cirkel.
At vide, at torvområdet var summen af dets sider, og at cirkelområdet var større, begyndte han at arbejde på at opnå tilnærmelser. Dette gjorde han ved at erstatte firkanten med en 6-sidet polygon og derefter arbejde med mere komplekse polygoner.
Archimedes var den første matematiker i historien til at nærme sig en seriøs beregning af tallet Pi.
Geometrien af kugler og cylindre
Blandt de ni afhandlinger, der udarbejder Archimedes arbejde i matematik og fysik, er der to volumener på geometrien af kugler og cylindre.
Dette arbejde omhandler bestemmelsen om, at overfladen af en hvilken som helst radius sfære er fire gange dens største cirkel, og at en sfære er to tredjedele af den cylinder, hvori den er indskrevet.
Inventos
Kilometerstanden
Også kendt som kilometer, var det en opfindelse af denne berømte mand.
Denne enhed blev bygget på basis af hjulprincippet, der aktiverer gear, når det drejer sig om at beregne den tilbagelagte afstand..
Ifølge samme princip konstruerede Archimedes flere typer odometre til militære og civile formål.
Det første planetarium
Baseret på vidneudsagn fra mange klassiske forfattere som Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sextus Empiricus og Lactancio, i dag mange forskere tilskriver Archimedes oprettelsen af den første rudimentære planetariske.
Det er en mekanisme, der består af en række "kugler", der formåede at efterligne planeternes bevægelser. Indtil videre er detaljerne i denne mekanisme ukendte.
Ifølge Cicero var planetarierne bygget af Archimedes to. I en af dem var landet og de forskellige konstellationer i nærheden af det repræsenteret.
I den anden, med en enkelt rotation, lavede solen, månen og planeterne deres egne uafhængige bevægelser i forhold til de faste stjerner på samme måde som de gjorde i en rigtig dag. I sidstnævnte kunne der desuden observeres efterfølgende faser og formørkelser af månen.
Skruen af Archimedes
Archimedes skruen er en enhed, der bruges til at transportere vand fra bund til top gennem en skråning ved hjælp af et rør eller en cylinder.
Ifølge den græske historiker Diodoro blev takket være denne opfindelse lettet vandingen af de frugtbare lande langs Nilen i det gamle Egypten, da de traditionelle værktøjer krævede en enorm fysisk indsats, som udmattede arbejderne.
Den anvendte cylinder er inde i en skrue af samme længde, som fastholder sammenkoblet et system af propeller eller finner, der udfører en roterende bevægelse, der drives manuelt af en roterende håndtag.
På denne måde klarer helikopterne at skubbe ethvert stof fra bunden op og danner en slags uendelig kredsløb.
Archimedes klo
Archimedes klo, eller den jernhånd, som den også er kendt, var et af de mest frygtelige krigsvåben, der blev skabt af denne matematiker, og blev den vigtigste for det sicilianske forsvar af de romerske invasioner.
Ifølge undersøgelser foretaget af professorer ved University of Drexel Chris Rorres (Institut for Matematik) og Harry Harris (Institut for Byggeri og Anlæg og Arkitektur), det var en stor løftestang, der havde en kæmper krog fastgjort til armen ved hjælp af en kæde der hang af den.
Gennem armen, så krogen faldt på fjenden skibet blev manipuleret, og målet var at tilslutte den og hæve det i en sådan grad, at frigivelsen blev opnået fuldstændig vælte eller gøre det at gå ned mod klipperne fra kysten.
Rorres og Harris præsenteret på symposiet "Maskiner og ekstraordinære strukturer antikken" (2001), en miniature repræsentation af dette apparat med titlen "En formidabel krigsmaskine: Konstruktion og drift af jern hånd Archimedes"
Til realiseringen af dette arbejde var de afhængige af argumenterne fra de antikke historikere Polibio, Plutarco og Tito Livio.
referencer
- ASSIS, A. (2008). Archimedes, tyngdepunktet og den første lov af mekanik [online]. Tilgænges 10. juni 2017 på bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [online]. Tilgænges den 9. juni 2015 på World Wide Web: books.google.co.ve/books.
- MOLINA, A. (2008). Forskningsmetoden for Archimedes of Syracuse: intuition, mekanik og udholdenhed [online]. Tilgænges den 10. juni 2017 på World Wide Webproduccioncientifica.luz.edu.
- O'Connor, J. & ROBERTSON, R. (1999). Archimedes of Syracuse [online]. Tilgænges 9. juni 2017 på history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimedes: hans liv, værker og bidrag til moderne matematik [online]. Hentet den 9. juni 2017 på lfunes.uniandes.edu.co.
- QUINN, L. (2005). Archimedes of Syracuse [online]. Adgang til 9 juni 2017 på math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). En formidabel krigsmaskine: Opførelse og drift af Archimedes 'Iron Hand [online]. Hentet den 10. juni 2017 på cs.drexel.edu.
- VITE, L. (2014). Archimedes princip [online]. Hentet den 10. juni 2017 på repository.uaeh.edu.mx.


