Transformed Laplace definition, historie, hvad det er til, egenskaber
den transformeret fra Laplace har i de seneste år været af stor betydning inden for ingeniørvidenskab, matematik, fysik, blandt andre videnskabelige områder, samt at have stor interesse i teoretisk, giver en enkel måde at løse problemer, der kommer fra videnskab og teknik.
Oprindeligt blev Laplace-transformen præsenteret af Pierre-Simon Laplace i hans studie om sandsynlighedsorienteringen og blev oprindeligt behandlet som et matematisk objekt af blot teoretisk interesse.

Nuværende applikationer opstår, når forskellige matematikere forsøgte at give en formel begrundelse til "operationelle regler" anvendt af Heaviside i studiet af ligninger af elektromagnetisk teori.
indeks
- 1 Definition
- 1.1 Eksempler
- 1.2 sætning (tilstrækkelige betingelser for eksistens)
- 1.3 Laplace transformation af nogle grundlæggende funktioner
- 2 historie
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 Egenskaber
- 3.1 Linearitet
- 3.2 Første oversættelse sætning
- 3.3 Andet oversættelses sætning
- 3.4 Skalaændring
- 3,5 ransformation af Laplace af derivater
- 3.6 Laplace transformation af integraler
- 3,7 Multiplikation med tn
- 3,8 Division af t
- 3.9 Periodiske funktioner
- 3.10 Adfærd af F (s), når s har tendens til uendelig
- 4 Omvendte transformationer
- 4.1 Øvelse
- 5 Anvendelser af Laplace-transformen
- 5.1 Differentialekvationer
- 5.2 Systemer af differentialligninger
- 5.3 Mekanik og elektriske kredsløb
- 6 referencer
definition
Lad f være en funktion defineret for t ≥ 0. Laplace transformen er defineret som følger:
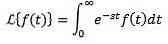
Det siges, at Laplace Transformen eksisterer, hvis det foregående integreret konvergerer, ellers siges det, at Laplace-transformen ikke eksisterer.
Generelt, for at betegne den funktion, som man ønsker at omdanne, bruges små bogstaver, og stor bogstaver svarer til dens omdannelse. På denne måde vil vi have:
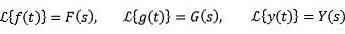
eksempler
Overvej den konstante funktion f (t) = 1. Vi har, at dens transformation er:
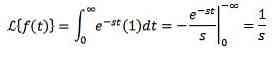
Når integralet konvergerer, er det altid forudsat at s> 0. Ellers s < 0, la integral diverge.
Lad g (t) = t. Din Laplace transform er givet af
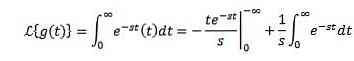
Ved at integrere ved dele og vide, at du-st det har tendens til at 0, når t har tendens til uendelig og s> 0, sammen med det foregående eksempel har vi det:
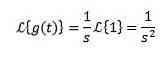
Transformationen kan eller måske ikke eksistere, for eksempel for funktionen f (t) = 1 / t det integral, der definerer dets Laplace-transformation, konvergerer ikke og derfor eksisterer dets transformation ikke.
Tilstrækkelige betingelser for at sikre, at Laplace-transformationen af en funktion f eksisterer, er at f er kontinuert i dele for t ≥ 0 og er af eksponentiel rækkefølge.
Det siges at en funktion er kontinuert i dele for t ≥ 0, når der for et hvilket som helst interval [a, b] med a> 0 er der et begrænset antal point tk, hvor f har diskontinuiteter og er kontinuert i hver underinterval [tk-1,tk].
På den anden side siges det, at en funktion er af eksponentiel orden c, hvis der er reelle konstanter M> 0, c og T> 0 sådan at:
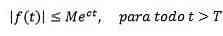
Som eksempler har vi f (t) = t2 er af eksponentiel rækkefølge, da | t2| < e3t for alle t> 0.
På en formel måde har vi følgende sætning
Stilling (Tilstrækkelige betingelser for eksistens)
Hvis f er en kontinuert funktion pr. Del for t> 0 og af eksponentiel rækkefølge c, er der Laplace transformen for s> c.
Det er vigtigt at fremhæve, at dette er en betingelse for tilstrækkelighed, det vil sige, at det kan være tilfældet, at der er en funktion, der ikke opfylder disse betingelser, og selv da er dens Laplace-transformation eksisteret.
Et eksempel på dette er funktionen f (t) = t-1/2 det er ikke kontinuert i dele for t ≥ 0, men dets Laplace-transformation eksisterer.
Laplace transformation af nogle grundlæggende funktioner
Den følgende tabel viser Laplace-transformerne af de mest almindelige funktioner.

historie
Laplace-transformationen skylder sit navn til Pierre-Simon Laplace, matematiker og fransk teoretisk astronom, der blev født i 1749 og døde i 1827. Hans berømmelse var sådan, at han blev kendt som Newton of France.
I 1744 viet Leonard Euler sine studier til integraler med formularen
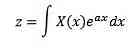
som løsninger af almindelige differentialligninger, men forlod hurtigt denne undersøgelse. Senere undersøgte Joseph Louis Lagrange, der stærkt beundrede Euler, også denne type integraler og relaterede dem til sandsynlighedsteorien.
1782, Laplace
I år 1782 begyndte Laplace at studere disse integraler som løsninger på differentialekvationer og ifølge historikere besluttede han i 1785 at omformulere problemet, som senere fødte Laplace-transformerne som de forstås i dag.
Efter at være blevet indført inden for sandsynlighedsregning, det var af ringe interesse for forskere på det tidspunkt og blev kun ses som en matematisk genstand for kun teoretisk interesse.
Oliver Heaviside
Det var i midten af det nittende århundrede, da den engelske ingeniør Oliver Heaviside opdagede, at differentialoperatører kan behandles som algebraiske variabler, hvilket giver deres moderne anvendelse til Laplace-transformerne.
Oliver Heaviside var en fysiker, elektroingeniør og matematiker englænder født i 1850 og døde i London i 1925. Under forsøget på at løse differentialligninger anvendes på vibrationer teori og undersøgelser ved hjælp af Laplace, begyndte at forme moderne anvendelser af Laplace-transformationerne.
Resultaterne udstillet af Heaviside spredte sig hurtigt i hele tidens videnskabelige samfund, men da dets arbejde ikke var stramt, blev det hurtigt kritiseret af mere traditionelle matematikere.
Hensigten med Heavisides arbejde med at løse fysiske ligninger gjorde hans metoder populære hos fysikere og ingeniører.
På trods af disse tilbageslag, og efter et par årtiers mislykkede forsøg, i begyndelsen af det tyvende århundrede det kunne give en streng begrundelse operationelle regler givet af Heaviside.
Disse forsøg udbetalte takket være forskellige matematikers indsats som bl.a. Bromwich, Carson, van der Pol..
egenskaber
Blandt egenskaberne ved Laplace-transformationen skiller sig følgende ud:
linearitet
Lad c1 og c2 være konstanter og f (t) og g (t) funktioner, hvis Laplace transformationer er henholdsvis F (s) og G (s), så skal vi:
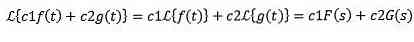
På grund af denne egenskab siges det, at Laplace-transformen er en lineær operatør.
eksempel
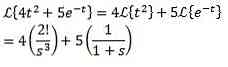
Første oversættelse sætning
Hvis det sker, at:
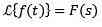
Og 'a' er et rigtigt tal, så:
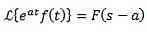
eksempel
Som Laplace-transformationen af cos (2t) = s / (s ^ 2 + 4) så:
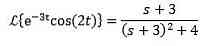
Anden oversættelse sætning
hvis
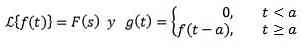
derefter
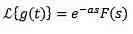
eksempel
Hvis f (t) = t ^ 3, så F (s) = 6 / s ^ 4. Og derfor omdannelsen af
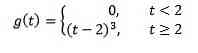
er G (s) = 6e-2s/ s ^ 4
Skalskift
hvis
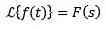
Og 'a' er et ikke-nul ægte, vi skal
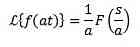
eksempel
Da transformationen af f (t) = sin (t) er F (s) = 1 / (s ^ 2 + 1), skal den være
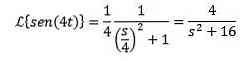
ransformation af Laplace af derivater
Hvis f, f ', f ", ..., f(N) er kontinuerlige for t ≥ 0 og er af eksponentiel rækkefølge og f(N)(t) er kontinuert i dele for t ≥ 0, derefter
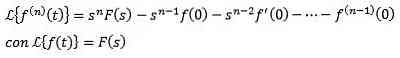
Laplace transformation af integraler
hvis
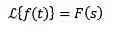
derefter
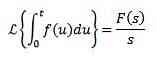
Multiplikation med tn
Hvis vi skal
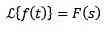
derefter
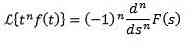
Division af t
Hvis vi skal
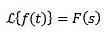
derefter
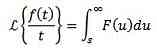
Periodiske funktioner
Lad f være en periodisk funktion med perioden T> 0, det vil sige f (t + T) = f (t), så
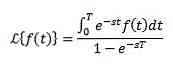
Adfærd af F (s), når s har tendens til uendelig
Hvis f er kontinuert i dele og eksponentiel rækkefølge og
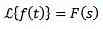
derefter
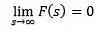
Inverse transformationer
Når vi anvender Laplace-transformen til en funktion f (t), får vi F (s), som repræsenterer denne transformation. På samme måde kan vi sige, at f (t) er den inverse Laplace-transformation af F (s) og er skrevet som
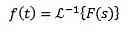
Vi ved, at Laplace-transformerne af f (t) = 1 og g (t) = t er F (s) = 1 / s og G (s) = 1 / s2 henholdsvis derfor må vi
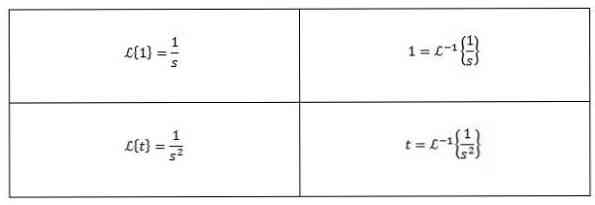
Nogle almindelige inverse Laplace-transformer er som følger

Desuden er den omvendte Laplace-transformation lineær, det vil sige det er opfyldt
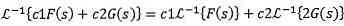
øvelse
finde
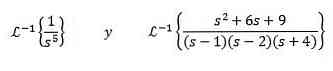
For at løse denne øvelse skal vi matche funktionen F (s) med en af de foregående tabeller. I dette tilfælde, hvis vi tager n + 1 = 5 og bruger linearitetsegenskaben for den inverse transformation, multipliceres og fordeles vi med 4! få
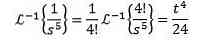
Til den anden inverse transformation anvender vi partielle fraktioner for at omskrive funktionen F (s) og derefter egenskaben for lineariteten, opnåelse
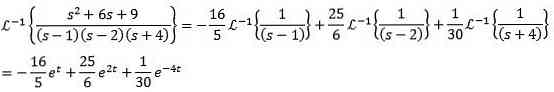
Som vi kan se fra disse eksempler er det almindeligt, at funktionen F (s), der vurderes, ikke er helt enig med nogen af de funktioner, der er angivet i tabellen. For disse tilfælde er det nok, som det er observeret, at omskrive funktionen, indtil den har nået den rigtige formular.
Anvendelser af Laplace transformen
Differentiale ligninger
Hovedapplikationen af Laplace-transformerne er at løse differentialligninger.
Ved anvendelse af transformationen af et derivat er det klart, at
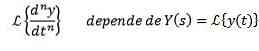
Og af n-1 derivaterne evalueret ved t = 0.
Denne egenskab gør transformationen meget nyttig til at løse initialværdiproblemer, hvor differentialekvationer med konstante koefficienter er involveret.
De følgende eksempler viser, hvordan man bruger Laplace-transformen til at løse differentialekvationer.
Eksempel 1
I betragtning af følgende initialværdiproblem
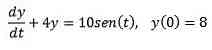
Brug Laplace transformen til at finde løsningen.
Vi anvender Laplace transformen til hvert medlem af differentialekvationen
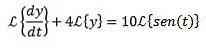
For ejendommen ved omdannelsen af et derivat, vi har
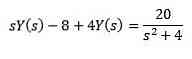
Ved at udvikle alle udtryk og clearing og vi er tilbage
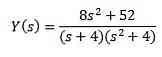
Brug partielle fraktioner til at omskrive den højre side af ligningen, vi opnår
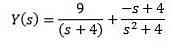
Endelig er vores mål at finde en funktion y (t), der opfylder differentialekvationen. Brug af den inverse Laplace-transformation giver os resultatet
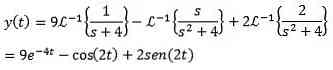
Eksempel 2
Løs
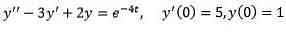
Som i det foregående tilfælde anvender vi transformationen på begge sider af ligningen og adskilt sigt efter sigt.
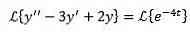
På denne måde har vi som følge heraf
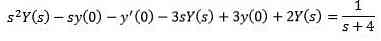
At erstatte de givne indledende værdier og rydde Y (s)
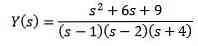
Ved hjælp af simple fraktioner kan vi omskrive ligningen som følger
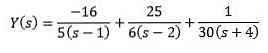
Og at anvende den omvendte transformation af Laplace giver os som følge heraf
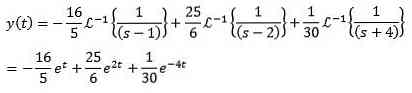
I disse eksempler kunne man komme til den forkerte konklusion, at denne metode ikke er meget bedre end de traditionelle metoder til at løse differentialekvationer.
Fordelene ved Laplace-transformen er, at det ikke er nødvendigt at anvende parametervariation eller bekymre sig om de forskellige tilfælde af den ubestemte koefficientmetode.
Udover at løse problemer med initialværdi ved denne metode, bruger vi fra begyndelsen de oprindelige betingelser, så det er ikke nødvendigt at udføre andre beregninger for at finde den konkrete løsning.
Differentiale ligningssystemer
Laplace-transformen kan også bruges til at finde løsninger på samtidige almindelige differentialligninger, som det følgende eksempel viser.
eksempel
løse
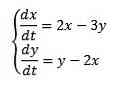
Med de oprindelige betingelser x (0) = 8 e og (0) = 3.
Hvis vi skal
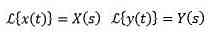
derefter
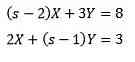
Løsning resultater i os
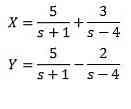
Og når du anvender den Laplace inverse transformation, har vi
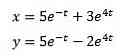
Mekanik og elektriske kredsløb
Laplace-transformationen har stor betydning i fysikken, og har hovedsagelig applikationer til mekaniske og elektriske kredsløb.
Et simpelt elektrisk kredsløb består af følgende elementer
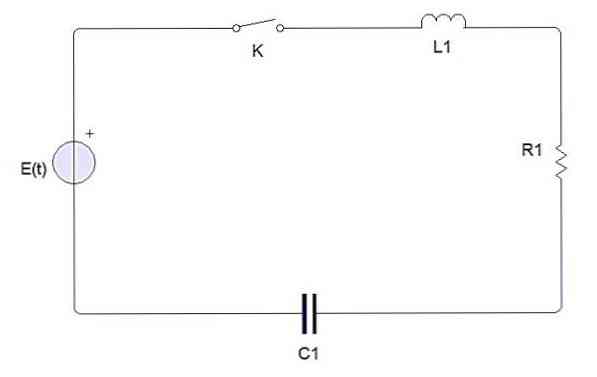
En switch, et batteri eller en kilde, en induktor, en modstand og en kondensator. Når kontakten er lukket, produceres der en elektrisk strøm, der betegnes af i (t). Kondensatorladningen betegnes med q (t).
Med Kirchhoffs anden lov skal spændingen produceret af kilden E til det lukkede kredsløb være lig med summen af hver af spændingsfaldene.
Den elektriske strøm i (t) er relateret til ladningen q (t) i kondensatoren ved i = dq / dt. På den anden side er spændingsfaldet defineret i hver af elementerne som følger:
Spændingsfaldet i en modstand er iR = R (dq / dt)
Spændingsfaldet i en induktor er L (di / dt) = L (d2q / dt2)
Spændingsfaldet i en kondensator er q / C
Med disse data og anvendelse af den anden Kirchhoff-lov til det lukkede enkle kredsløb opnås en anden ordens differentialekvation, der beskriver systemet og giver os mulighed for at bestemme værdien af q (t).
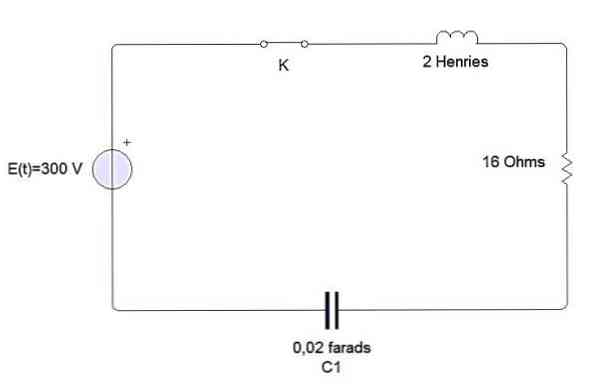
eksempel
En induktor, en kondensator og en modstand er forbundet med et batteri E som vist i figuren. Induktoren er af 2 henries, kondensatoren på 0,02 farads og modstanden på 16 onhm. På tidspunktet t = 0 er kredsløbet lukket. Find belastningen og strømmen til enhver tid t> 0 hvis E = 300 volt.
Vi har, at differentialekvationen, der beskriver dette kredsløb, er følgende
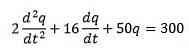
Hvor de oprindelige betingelser er q (0) = 0, i (0) = 0 = q '(0).
Ved anvendelse af Laplace transformen får vi det
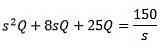
Og rydde Q (t)
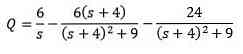
Derefter anvender vi den omvendte Laplace-transformation, vi har
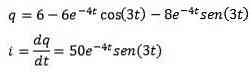
referencer
- G. Holbrook, J. (1987). Laplace transformation til elektronik ingeniører. Limusa.
- Ruiz, L. M., & Hernandez, M. P. (2006). Differentialekvationer og Laplace-transformation med applikationer. Editorial UPV.
- Simmons, G. F. (1993). Differentialekvationer med applikationer og historiske noter. McGraw-Hill.
- Spiegel, M.R. (1991). Laplace Transforms. McGraw-Hill.
- Zill, D. G., & Cullen, M.R. (2008). Differentialekvationer med problemer med værdier ved grænsen. Cengage Learning Editores, S.A..


