Heptagonal prisme funktioner og hvordan man beregner volumen
en heptagonal prisme er en geometrisk figur, der som navnet antyder involverer to geometriske definitioner, der er: prisme og heptagon.
Et "prisme" er en geometrisk figur, der er begrænset af to baser, der er lige og parallelle polygoner, og deres sideflader er parallelogrammer.
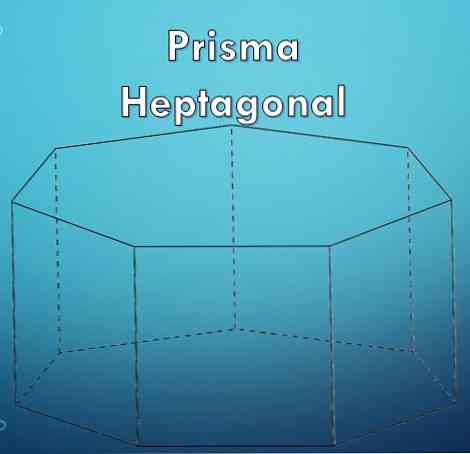
En "heptagon" er en polygon, der er dannet af syv (7) sider. Da en heptagon er en polygon, kan det være, at det er regelmæssigt eller uregelmæssigt.
En polygon siges at være regelmæssig, hvis alle sider har samme længde og interne vinkler er de samme, også kaldet ligesidede polygoner; ellers er det sagt at polygonen er uregelmæssig.

Karakteristik af et Heptagonal Prism
Følgende er visse funktioner, der har et heptagonal prisme såsom: dets konstruktion, egenskaber af dets baser, området af alle dets ansigter og dets volumen.
1- Konstruktion
For at konstruere et heptagonal prisme er der brug for to heptagoner, som vil være dens baser og syv parallelogrammer, en på hver side af heptagonen.
Start med at tegne en heptagon, og træk derefter syv lodrette linjer af samme længde, som kommer fra hver af sine hjørner.
Endelig tegnes en anden heptagon, så dens hjørner falder sammen med enden af linjerne, der er tegnet i det foregående trin.
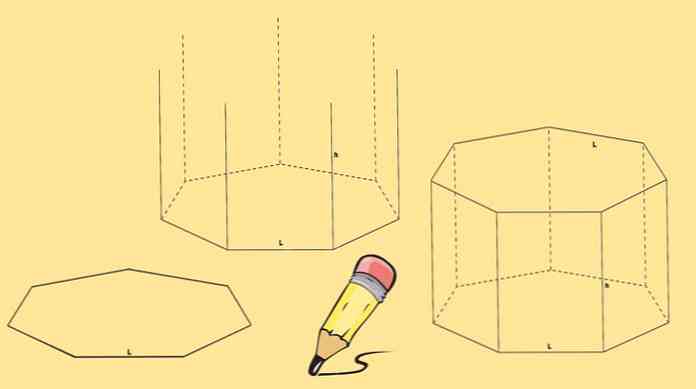
Det heptagonale prisme, der er trukket ovenover, kaldes et lige heptagonal prisme. Men du kan også have en skrå heptagonal prisme som den i den følgende figur.

2- Egenskaber af dets baser
Da baser er heptagoner, disse opfylder antallet af diagonal er D = nx (n-3) / 2, hvor "n" er antallet af polygonens sider; i dette tilfælde har vi det D = 7 × 4/2 = 14.
Vi kan også se, at summen af de indre vinkler af enhver heptagon (regelmæssig eller uregelmæssig) er lig med 900º. Dette kan verificeres af følgende billede.
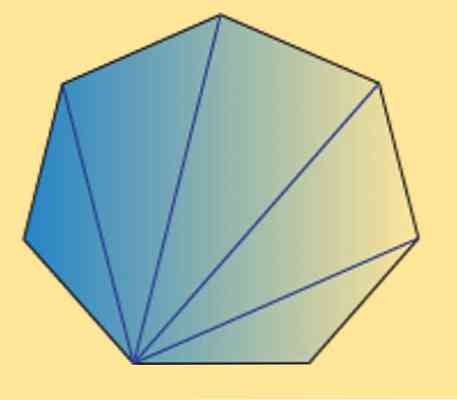
Som det kan ses, er der fem indre trekanter, og ved hjælp af summen af de indvendige vinkler af en trekant er lig med 180, kan man opnå det ønskede resultat.
3- Areal er nødvendigt for at bygge et Heptagonal prisme
Som baser er heptagoner og to sider er parallelogrammer syv, det areal, der kræves for at opbygge en sekskantet prisme er lig med + 2xH 7XP hvor "H" er arealet af hver heptagon og "P" arealet af hver parallelogram.
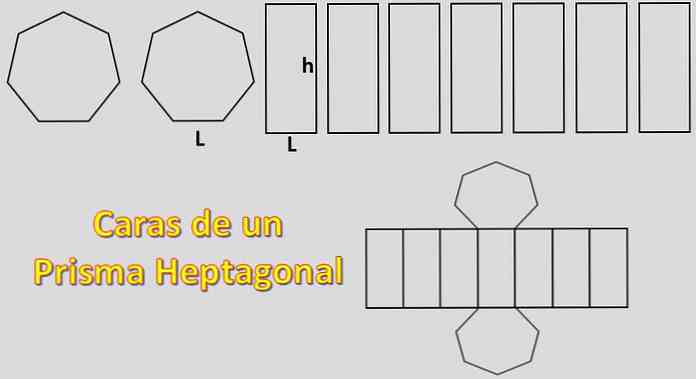
I dette tilfælde beregnes området for en almindelig heptagon. For dette er det vigtigt at kende definitionen af apothema.
Apotem er en vinkelret linje, der går fra midten af en regelmæssig polygon til midtpunktet på nogen af dens sider.
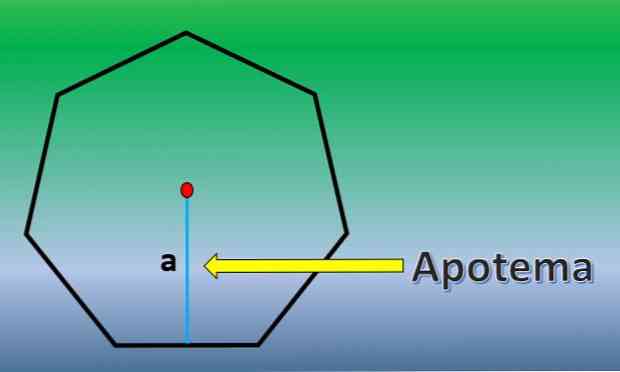
Engang kendt APOTEMA område har at Heptagon er H = 7xLxa / 2, hvor "L" er længden af hver side og "en" længde APOTEMA.
Området af et parallelogram er let at regne, defineres som P = Lxh, hvor "L" er den samme længde af siden af heptagonen og "h" er prisens højde.
Det konkluderes, at nødvendig for at opbygge et heptagonal prisme materiale (regelmæssigt) beløb er 7xLxa + 7xLxh, dvs. 7XL (a + h).
4- volumen
Når området af en base og højden af prismer er kendt, defineres volumenet som (basisareal) x (højde).
I tilfælde af et heptagonal prisme (med regelmæssig basis) har det, at dets volumen er V = 7xLxaxh / 2; kan også skrives som V = Pxaxh / 2, hvor "P" er omkredsen af den regelmæssige heptagon.
referencer
- Billstein, R., Libeskind, S., & Lott, J.W. (2013). Matematik: en problemløsende tilgang til grundlærere. López Mateos Editores.
- Fregoso, R. S., & Carrera, S.A. (2005). Matematik 3. Editorial Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Matematik 6. Editorial Progreso.
- Gutiérrez, C.T., & Cisneros, M.P. (2005). 3. matematik kursus. Editorial Progreso.
- Kinsey, L., & Moore, T. E. (2006). Symmetri, form og rum: En introduktion til matematik gennem geometri (illustreret, genoptryk ed.). Springer Science & Business Media.
- Mitchell, C. (1999). Blændende Math Line Designs (Illustrated ed.). Scholastic Inc.
- R., M. P. (2005). Jeg tegner 6º. Editorial Progreso.


